大数据与工业大数据（番外二）：从贝叶斯到卡尔曼

上一期《大数据与工业大数据番外一》中，我简单给大家科普了一下贝叶斯理论及贝叶斯方法。重点强调了一下贝叶斯方法在平衡先验知识及测量数据上优越性，从而使它在性能上能超过传统经典的方法。

然而，正所谓“花无百日红”（这个引用好像有点不太恰当：））。贝叶斯理论的确很好，但并不是说没有问题。

在这一篇番外里，我将继续就贝叶斯方法这个话题进行展开，谈一谈它在现实应用中的局限，以及大家是如何来解决这些问题，从而为它带来现实应用的价值及活力。

01

Whats the root cause?

的问题

贝叶斯理论

出在哪儿？

贝叶斯理论的确很好，但也仅是理论很好。一用到实际问题的解决中，问题就出现了。

在上文中我们提到了，贝叶斯理论的核心在于后验概率函数。

基于贝叶斯理论的贝叶斯方法都是在这个后验概率上做文章，无论是最大后验概率方法还是最小化均方误差的方法。

问题就出在这个后验概率函数上。我们先来看看这个后验概率函数长啥样：

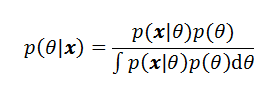
公式看起来非常简单。可大家注意到了吗？在分母上有个积分。

大家学过微积分，应该知道：微分比较好计算，但积分并不是什么函数都能算得出来的（数值解法不算）。

也就是说，即使分子上的似然函数的形式和先验概率函数的形式都已知，要算出后验概率函数还得求解分母上的复杂函数。

不幸的是，分母上的这个函数的形式除了少数特殊函数，这个复杂的积分一般是解不出来的。更何况，一般情况下，未知参数?可能不止一个，也就意味着分母会是一个多重积分，这样就更别指望能解出来了。

02

Whats the solution?

实际应用

贝叶斯理论的

解决方案

看到这里是不是有点绝望？

贝叶斯这种大家只负责提理论，像实际应用这种事就交给卡尔曼这样的晚辈去做了。（哈哈，我瞎说的。）

当然，这么好的理论放着不用多可惜啊。

后来的人们一直试图在各个领域中应用贝叶斯方法。

一般而言有两个途径。

1

寻找可以解算出后验概率函数的特殊概率函数形式，当然要确保这种特殊函数在实际中是有应用价值的。

2

利用近代计算能力的飞速发展，寻找“聪明”的数值解法。

第一条路出来的，其中最著名的就是卡尔曼滤波器了；

而第二条路出来的，其中最著名的就是Particle Filter（粒子滤波器，中文还有更好的翻译吗？）（这是我随意说的。 ^_^ 没有谁评选过哪一个是最著名的。不过，卡尔曼滤波器的地位应该是不用质疑的。）

How about

particle Filter?

先扯两句Particle Filter。在我当年做博士论文那会儿，它还是超有名的。

我在博士期间发表的最后一篇期刊文章就是关于Particle Filter的。到现在，我已经在工业界浸染了10年。这十年间，有关Particle Filter的应用却完全没有听到过。（可能是我的领域较窄。若有相关信息的同学，欢迎共享一下）。

And

Kalman Fileter?

卡尔曼滤波的实际应用却总是碰见，无论是在控制、虚拟测量、参数估计等等，都有它的身影。

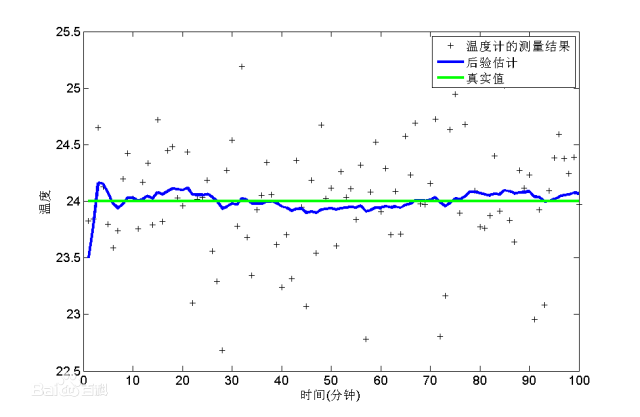
关于卡尔曼滤波器，介绍它的文章太多了，我就不赘述了。这里简略地讨论它的几个关键点。

壹

要了解卡尔曼滤波，必须先要了解Sequential Bayes Theory及Sequential Bayes估计（有些场合也叫做Recursive Bayes估计）。这是贝叶斯方法在解决时序问题或动态问题是的一个特殊应用场景。卡尔曼滤波器是Sequ Bayes 估计的一个特殊形式。

贰

卡尔曼滤波是假设了：过程噪声及测量噪声都满足高斯分布，且信号和噪声间是线性关系。为啥要有这个假设呢？回到前面的后验概率函数，主要难点在于积分难解。这个假设就是为了让积分里的函数是高斯函数的形式。对于高斯函数这种特殊形式，它的n重积分都是可以轻松写出来的。

叁

当然不用忘了，卡尔曼滤波还离不开马尔科夫链的状态假设（又是一个以人名命名的名词）。

肆

有了上面这些假设后，你只要把高斯函数的形式代入后验概率函数的公式中，然后对它求导数，并让导数等于零，经过一番推导后，你就会惊讶地发现，结果就是你熟悉（而又陌生）的卡尔曼滤波器的形式了。

（当然，这个推导并不简单。想当年，我可是认认真真地推导了一番，就是为了看看结果到底是不是卡尔曼滤波器的形式。其过程还是颇费了些周折的。）

03

Who is Kilman?

卡尔曼大师

何方神圣？

好了，文章到此也该结束了。最后谈谈这个卡尔曼到底是何许人也。

当年，刚接触到卡尔曼滤波器时，想当然地以为，卡尔曼也是和贝叶斯一样，不属于我们这个时代的人物。直到有一天，我看见了下面这张照片：

OMG!

卡尔曼竟然和奥巴马同框了！而且还向他鞠躬！（不要误会，我不是说奥巴马有啥问题，我只是没想到自己竟然有幸和这位伟大的数学家有几十年共同生活在地球上的经历。。。）

好吧，小伙伴们，是否觉得卡尔曼滤波器没那么遥远了？

最后上一张卡尔曼老爷爷当年的帅照，借此也让大家缅怀一下这位一代宗师：伟大的、划时代的数学家。

二当家

有话说

古语云：“磨刀不误砍柴工”。想真正地了解工业大数据，看懂其里面的花花世界，还是得先掌握必要的统计 知识和具备一定的数学功底。

上一期，通过贝叶斯老大人，了解了“贝叶斯理论”。这期，逍遥公子请出了一代数学宗师卡尔曼！目的就是让大家在熟悉的专业名词面前，进而轻松地了解“后验概率函数”的局限性以及其怎么在实际应用中发光发热。

So far, 逍遥公子这两篇番外的深入浅出的理论剖析，是不是让你感觉原本烧脑的统计学知识变得有一点亲民、接地气了？

下一期,逍遥公子将回归正题，继续跟大家讨论“工业大数据”的话题。

未完待续