大数据与工业大数据（番外 一）：贝叶斯方法与最大后验概率估计

在贝叶斯方法出现之前，在对所关注参数的值进行估计时，用的是传统经典的方法，即：基于统计的方式。

在正式阐述贝叶斯方法与先验知识之前，容我先带大家温习一下：传统的统计方法是什么样的？

Q1

传统的统计方法是什么样的？

假设需要估计一个变量的值，它的值是确定的，但却未知。

举一个常见的例子加以说明。

工业场合需要用传感器测量很多现场的变量。例如：压力、温度、流量等等。通常情况下，这些变量都或多或少地受到现场或采集设备噪声的影响，导致其测量值不是一个固定值，如下图所示。

测量值的分布

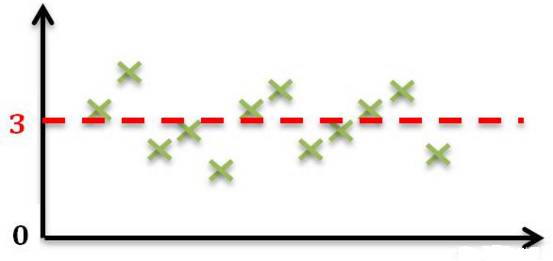
为了估计出测量值，我们通常对测量值先进行采样，然后计算出平均值，作为其测量的估计值。

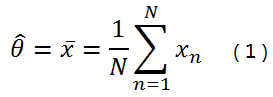
其中：N是采集的样本个数；Xn是测量值。

这就是按照传统经典统计方法中的最小化平均误差所得到的估计结果。

这种方法存在一个问题：如果测量的样本数不够多，或者样本中有些值受到了干扰而出现错误时 （如下图），就会出现不期望的计算误差。

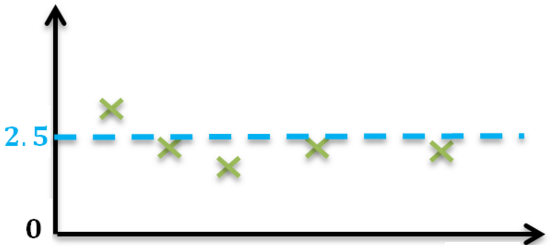
这时，如果仍然采用传统的基于统计的方法进行计算，误差就很难避免，也找不到一个系统的方法去真正地解决它。

Root cause就是：它仅仅依赖测量到的信息得出估算的结论。

Q2

更好的解决方案：贝叶斯方法

这种情况下，贝叶斯方法就是一个很好的备选方案。它通过引入先验知识来提高了测量值的估计精度。

那么，贝叶斯方法是怎么工作的呢？

当我们采用贝叶斯方法时，前提是假设待估计的变量不是一个确定值，而是一个随机变量。我们要做的，就是估计它的一个实现的值。（略拗口，后面就能慢慢清楚了。 ^_^）

既然未知参数是个随机变量，它就会有个先验概率分布。

未知参数的先验知识能通过先验概率影响最终的估计值，从而获得比传统方法更高的估计精度。这个结论在一定程度上是可以被证明的。

接下来，为了让大家更好地理解贝叶斯方法，我们还是回到前面那个的例子，做一点小小的推导进一步解释一下。

Q3.1

贝叶斯方法

先验概率 -> 最大后验概率估计

我们这里要做的事其实很简单：假设一个直流分量A受到了一些加性的高斯白噪声的影响。我们需要估计A的值。

按照贝叶斯理论的前提条件，A是一个随机变量，我们假设它的先验概率函数是一个高斯分布，其均值为μA，标准方差为σA，即

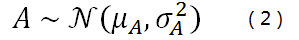
接下来，需要引入另一个概念：按照贝叶斯理论，最佳的估计器是最大后验概率估计。（忍了忍，还是不把后验概率的公式写出来，免得公式太多，吓着大家^-^, 感兴趣的自己Google吧。）

根据贝叶斯理论，按照最大后验概率估计，我们能得出 A的估计值是：

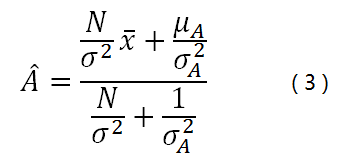
看到这个结果，大家是不是有点头晕？ 先坚持住，容我慢慢道来，马上就要柳暗花明了。

我们只需把这个公式稍微整理一下。先定义一个变量α，如下式。

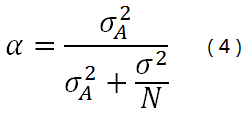
你心里兴许在问：这是什么鬼？别急，好戏来了 ^_^

引入变量α后，式（3）重新写成了：

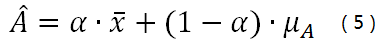
这下看着，是不是舒服多了？ ^_^。

其中：第一项的x_bar是所有测量值的平均值，反映了测量值的信息。

第二项： μA是先验概率函数的均值，反映了先验知识的信息。

所以，最终的估计值A 既不只依赖测量值，也不只相信先验信息，而是测量值平均值和先验概率函数均值的一个加权和。其中，权重就是α。

怎么样？到这儿，是不是看出点门道了？

再来仔细看一下这个权重值α。

我们发现它和样本个数N 有关系。

如果N很大，α趋近于1，估计值A也更接近于x_bar- 测量值的平均值。这表明在样本个数很多的情况下，我们会更倾向于相信测量值的信息。

而反过来，如果N很小或者样本的平均方差σA很大时，α会趋近于0，估计值A则更接近于先验均值 μA。这表明，当样本个数过小或者测量值受噪声干扰过大时，我们则更倾向于相信先验知识。

这下有点清楚了吧？

Q3.2

为什么根据贝叶斯最大后验概率估计出的结果，其精度总是高于传统方法？

衡量估计器精度的重要指标是均方误差。

经过推导不难得出，贝叶斯估计方法结果的均方误差是：

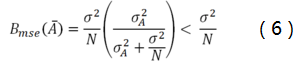
可见，贝叶斯方法的均方误差总是小于传统方法的均方误差。

Q3.3

贝叶斯方法的精妙之处在哪里？

其实，在数据分析中，运用先验知识得出更好的结果，是一个很常用的方法。

贝叶斯方法的精妙之处就在于：它提供了一种具体的、在某种情况下最优的、如何利用先验知识的方法，能获得比传统数据分析更高的误差精度。

当然，能利用先验知识提高测量值的估计精度的方法还有很多，贝叶斯理论也不能完全涵盖。这就需要大家在自己的实际工作中去发掘，去挖掘。

未

完

待

续

END